Recursos para ensinar filosofia
Quadrado de oposições
O quadrado de oposições representa as relações existentes entre os quatro tipos de proposições categóricas. No canto superior esquerdo temos a proposição universal afirmativa (A), no canto superior direito a universal negativa (E), no canto inferior esquerdo a particular afirmativa (I) e no canto inferior direito a universal negativa (O).
Conhecer o quadrado de oposições e as relações existentes entre cada uma das proposições que o compõem serve para podermos fazer inferências e raciocinar adequadamente sobre classes de objetos.
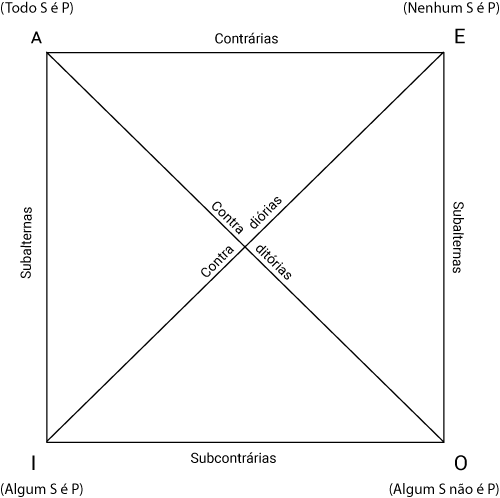
A imagem acima representa as quatro relações (contraditórias, contrárias, subalternas e subcontrárias) existentes entre os quatro tipos de proposições categóricas. Dizemos que A e E são contrárias, I e O são subcontrárias, A e I são subalternas, assim como E e O e A e O, por um lado, e E e I, por outro, são proposições contraditórias.
Agora vamos analisar cada uma dessas relações e o que podemos aprender com elas.
Proposições contraditórias
Considere as duas afirmações abaixo:
Todos os advogados são bem pagos (A).
Alguns advogados não são bem pagos (O).
Se uma é verdadeira a outra é falsa. Se é verdade todos os advogados são bem pagos, então é falso que alguns não são bem pagos. Se é verdade que alguns advogados não são bem pagos, então é falso que todos os advogados são bem pagos. Pelo fato de essas afirmações não poderem ser verdadeiras ao mesmo tempo, são chamadas de contraditórias.
Proposições universais afirmativas e particulares negativas são contraditórias, assim como universais negativas e particulares afirmativas.
Vamos ver mais um exemplo desse caso:
Nenhum morcego representa risco à saúde (E).
Algum morcego representa um risco à saúde (I).
Por serem duas proposições contraditórias, sabemos que, se uma é verdadeira, a outra é falsa. Se é verdade que nenhum morcego representa um risco à saúde, então é falso que algum morcego representa um risco à saúde. Ao contrário, se a segunda proposição for verdadeira, a primeira é falsa.
Proposições contrárias
Analise o exemplo abaixo:
Todos os políticos são corruptos (A).
Nenhum político é corrupto (E).
A primeira proposição é universal afirmativa (A) e a segunda é universal negativa (E). Essas proposições são contrárias, porque pelo menos uma tem que ser falsa. Se a primeira é verdadeira, então a segunda é falsa. Se a segunda é verdadeira, a primeira tem que ser falsa. No entanto, como ocorre nesse exemplo, proposições contrárias podem ser ambas falsas ao mesmo tempo, já que tanto a primeira quanto a segunda afirmação são falsas.
Proposições subalternas
A relação de subalternidade existe entre uma proposição universal afirmativa (A) e particular afirmativa (I), por um lado, e universal negativa (E) e particular negativa (O) por outro.
Todos os gatos são peludos (A).
Alguns gatos são peludos (I).
Nesse caso, se a proposição A é verdadeira, a proposição I também tem que ser verdadeira. Porém, se A é falso, I pode ser verdadeiro ou falsa. Se é verdade todos os gatos são peludos, então também é verdade que alguns gatos são peludos. Porém, se é falsa que todos os gatos são peludos, pode ser que existam alguns que sejam. Então, nesse caso, o valor I fica indeterminado.
Se, por outro lado, I é falso, A também deve ser falso. Se é falso que alguns gatos são peludos, então é necessariamente falso que todos os gatos são peludos. Se, ao contrário, é verdade que alguns gatos são peludos, não é possível saber se é verdade que todos os gatos são peludos. O valor de verdade de A é indeterminado.
Considere agora um exemplo com proposições negativas:
Nenhum pescador fala a verdade (E).
Algum pescador não fala a verdade (O).
As relações lógicas existentes entre essas duas proposições são as mesmas identificadas entre as proposições afirmativas A e I acima. Se E é verdadeira, então O é verdadeira. Se E é falsa, então o valor de verdade de O é indeterminado. Se O é falsa, por outro lado, E também é falsa. Se O é verdadeira, o valor de verdade de E é indeterminado.
Relações entre proposições subcontrárias
| Se A é verdadeira | I é verdadeira |
| Se E é verdadeira | O é verdadeira |
| Se A é falsa | I é indeterminada |
| Se E é falsa | O é indeterminada |
| Se I é verdadeira | A é indeterminada |
| Se O é verdadeira | E é indeterminada |
| Se I é falsa | A é falsa |
| Se O é falsa | E é falsa |
Proposições subcontrárias
Por fim temos as relações lógicas entre proposições subcontrárias particular afirmativa (I) e particular negativa (O).
Considere um exemplo:
Algum animal é um gato (I).
Algum animal não é um gato (O).
Proposições subcontrárias podem ser ambas verdadeiras ao mesmo tempo, mas não podem ser ambas falsas. Assim, se I é verdadeira, O pode ser verdadeira ou falsa. Mas se I for falsa, então O é verdadeira.
Fazendo inferências com o quadrado de oposições
A tabela abaixo é uma síntese das inferências imediatas que é possível fazer a partir das relações lógicas existentes entre os tipos de proposições.
| Proposição | Inferência imediata |
| Se A é verdadeira | E é falso, I é verdadeiro e O é falso |
| Se E é verdadeira | A é falso, I é falso, e O é verdadeiro |
| Se I é verdadeira | E é falso e A e O são indeterminados |
| Se O é verdadeira | A é falso e I e E são indeterminados |
| Se A é falsa | O é verdadeira, E e I são indeterminados |
| Se E é falsa | I é verdadeira, A e O são indeterminados |
| Se I é falsa | A é falsa, E é verdadeira e O é verdadeira |
| Se O é falsa | A é verdadeira, E é falsa e I é verdadeira. |
Existem ainda outros três tipos de inferências imediatas que podem ser feitas com as proposições categóricas, essas são chamadas de conversão, obversão e contraposição e são o tema do próximo artigo.
